A Walkthrough Example of Quicksort
A step-by-step walkthrough of performing Quicksort on a simple array to better understand it’s workings.
Contents
Quicksort, Slowly
Starting with an array:
We first set the values low and high that determine the subset of the array in which we’ll be working. With this being the first pass, low will be 0 and high will be length - 1.
We then ask the return condition.
Is low ≥ high ?
No! We’ve only just started! But this would be true if the length of the array was 0 or 1 because an array of length 0 or 1 is always sorted. We’d then return, breaking the cycle.
We need to find where our first split will be. This will be around the pivot.
We’ll set pivot to array[high]. For now, that’s the last item in the array.
We’ll also set index to low - 1.
We’ll then loop through the array, from low to high.
Start!
Is item ≤ pivot ?
Yes! Increase index by 1 and swap the values of index and item.
Next Item!
Is item ≤ pivot ?
Yes! Increase index by 1 and swap the values of index and item.
Next Item!
Is item ≤ pivot ?
No!
Next Item!
Is item ≤ pivot ?
Yes! Increase index by 1 and swap the values of index and item.
Next Item!
Is item ≤ pivot ?
Yes! Increase index by 1 and swap the values of index and item.
Next Item!
Is item ≤ pivot ?
No!
Next Item!
Is item ≤ pivot ?
Yes! Increase index by 1 and swap the values of index and item.
Finished! Increase index by 1 and swap index and pivot.
The item at pivot is now sorted.
The array is now split at pivot.
Items to the left are all less than or equal to pivot.
Items to the right are all greater than pivot.
We’ll branch off to the left first.
With pivot index - 1 as high, go again!
Is low ≥ high ?
No!
Set pivot to array[high] and index to low - 1
Start!
Is item ≤ pivot ?
Yes! Increase index by 1 and swap the values of index and item.
Next item!
Is item ≤ pivot ?
No!
Next Item!
Is item ≤ pivot ?
No!
Next Item!
Is item ≤ pivot ?
No!
Finished! Increase index by 1 and swap index and pivot.
The item at pivot is now sorted.
The array is now split at pivot.
Items to the left are all less than or equal to pivot.
Items to the right are all greater than pivot.
We’ll continue down this path, branching off to the left first.
With pivot index - 1 as high, go again!
Is low ≥ high ?
Yes! This item is already sorted!
We’ll branch off to the right now.
With pivot index + 1 as low, go again!
Is low ≥ high ?
No!
Set pivot to array[high] and index to low - 1
Start!
Is item ≤ pivot ?
Yes! Increase index by 1 and swap the values of index and item.
Next Item!
Is item ≤ pivot ?
Yes! Increase index by 1 and swap the values of index and item.
Finished! Increase index by 1 and swap index and pivot.
The item at pivot is now sorted.
The array is now split at pivot.
Items to the left are all less than or equal to pivot.
Normally, there would be a second branch where the items to the right are all greater than pivot. Though, in this case, the pivot is the last item in the subset and there are no items to the right! So there is only the branch to the left.
We’ll continue down this path.
With pivot index - 1 as high, go again!
Is low ≥ high ?
No!
Set pivot to array[high] and index to low - 1
Start!
Is item ≤ pivot ?
Yes! Increase index by 1 and swap the values of index and item.
Finished! Increase index by 1 and swap index and pivot.
The item at pivot is now sorted.
The array is now split at pivot.
Items to the left are all less than or equal to pivot.
There is no right branch.
We’ll continue down this path.
With pivot index - 1 as high, go again!
Is low ≥ high ?
Yes! This item is already sorted!
We’ve finished the original left branch! Let’s move on to the right.
With pivot index - 1 as high, go again!
Is low ≥ high ?
No!
Set pivot to array[high] and index to low - 1
Start!
Is item ≤ pivot ?
No!
Finished! Increase index by 1 and swap index and pivot.
The item at pivot is now sorted.
The array is now split at pivot.
There is no left branch.
Items to the right are all greater than pivot.
We’ll continue down this path.
With pivot index - 1 as high, go again!
Is low ≥ high ?
Yes! This item is already sorted!
All finished!
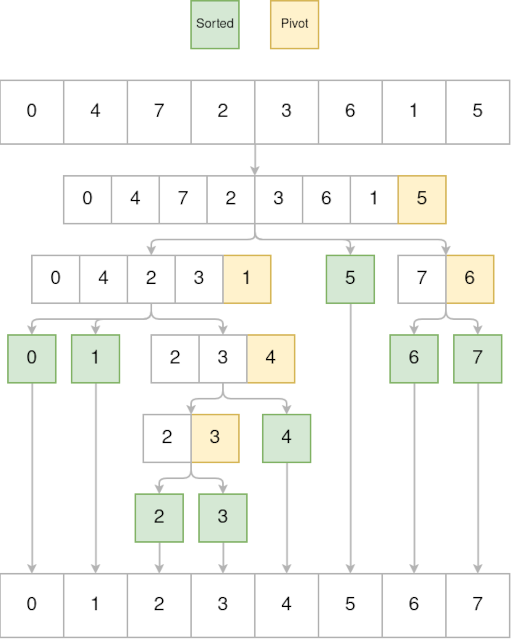
We can visualize the result as a tree:
Write it in Python!
# quicksort.py
import time
from typing import List
def quicksort(array: List[int]) -> List[int]:
def _quicksort(array: List[int], low: int, high: int):
if low >= high:
return
pivot_index = _partition(array, low, high)
_quicksort(array, low, pivot_index-1)
_quicksort(array, pivot_index+1, high)
def _partition(array: List[int], low: int, high: int) -> int:
pivot = array[high]
index = low - 1
for item in range(low, high):
if array[item] <= pivot:
index += 1
temp = array[item]
array[item] = array[index]
array[index] = temp
index += 1
array[high] = array[index]
array[index] = pivot
return index
_quicksort(array, 0, len(array)-1)
return array
array = [0, 4, 7, 2, 3, 6, 1, 5]
start_time = time.time()
sorted_array = quicksort(array[:])
print(f'{array} → {sorted_array} in {(time.time() - start_time) * 1000:.3f}ms')$ python quicksort.py
[0, 4, 7, 2, 3, 6, 1, 5] → [0, 1, 2, 3, 4, 5, 6, 7] in 0.008ms0.008ms?! Maybe we’ll let the computer handle it from now on...